牛顿问题是牛顿在《普通算术》一书中提出来的,也就是大家所熟知的牛吃草问题。同时,牛吃草问题也是公考行测科目中数量关系模块的题型之一,从近些年考试的真题来看,难度并不是很大,是大多数考生可以拿到分数的题型。下面通过举例帮助大家更好地理解这个题型。
表1 牛吃草题型情况分析表
| 原有草量(Y) | 牛的数量(N) | 每天长草量(X) | 消耗时间(T) |
| 1000份 | 40头 | 0 | 25天 |
| 情况一:假设每头牛每天消耗1份草,则40头牛每天共消耗40份 草,因此1000份草,25天可以消耗完。 |
|||
| 1000份 | 40头 | 20份 | 50天 |
| 情况二:假设每头牛每天消耗1份草,则40头牛每天共消耗40份草,同时每天生长20份草,因此每天实际消耗20份草,所以1000份草,50天可以消耗完。 | |||
| 1000份 | 40头 | 20份 | 10天 |
| 情况三:假设每头牛每天消耗3份草,则40头牛每天共消耗120份草,同时每天生长20份草,因此每天实际消耗100份草,所以1000份草,10天可以消耗完。 | |||

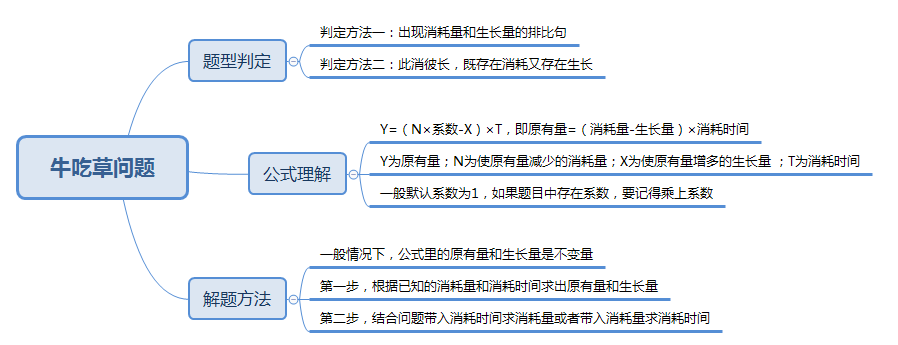
通过上面的表格,我们可以得到牛吃草问题的公式Y=(N系数-X)T,其中Y表示原有草量;N系数表示消耗量,N为牛的数量,我们默认每头牛每天吃1份草,即系数默认为1;X表示长草量,即生长量;T为消耗时间。因此牛吃草公式可以总结为原有量=(消耗量-生长量)消耗时间,即原有量=净消耗消耗时间。
表2 牛吃草题型判定表
| 题型特征一 | 题目中出现关于消耗量和生长量的排比句 |
| 题型特征二 | 题中既存在消耗又存在生长,即有消有长 |
| 备注:以上是两种判定牛吃草问题的方法,并非要同时满足;使原有量减少的量为消耗量;使原有量增多的量为生长量;一般情况下,公式中原有量和生长量是固定不变的。 | |
下面我们通过例题实际操作一下:
【例1】一片牧场,12头牛吃4天,9头牛吃6天,多少头牛2天就能吃完?( )
A.20 B.21
C.22 D.23
解析:12头牛每天消耗12份草,生长量为X,则净消耗为12-X,即原有量=(12-X)4;9头牛每天消耗9份草,净消耗为9-X,即原有量=(9-X)6。利用连等式原有量=(12-X)4=(9-X)6,解得原有量Y=36,生长量X=3,则36=(N-3)T,当T=2时,N为21,需要21头牛。答案为B。
【例2】一条船因触礁船体破了一个洞,海水均匀地进入船内。发现船漏时,船已经进了一些水。如果13人舀水,3小时可以舀完;如果6人舀水,10小时可以舀完。如果在2小时内舀完水,最少需要多少人?( )
A.15 B.16
C.17 D.18
解析:根据“船已经进了一些水”,可知原来船上存在一定量的水,即原有量Y;因为“海水均匀地进入船内”,所以进水为使水量增多的生长量X;根据“13人舀水,3小时舀完”,可以确定舀水的人是使水量减少的消耗量。利用连等式(13-X)3=(6-X)10,解得原有量=30,生长量=3,即30=(N-3)T,当T=2时,N为18,需要18个人。答案为D。
【例3】一艘轮船发生漏水事故,立即安装两台抽水机向外抽水,此时已进水800桶。一台抽水机每分钟抽水18桶,另一台每分钟抽水14桶,50分钟把水抽完。每分钟进水多少桶?( )
A.16 B.18
C.20 D.21
解析:此题在前两道例题基础上进行了一定的变化,出现了系数,并不是默认每头牛每天吃一份草,而是“有两头牛,一个每天吃18份草,一个每天吃14份草”。根据公式得到等式800=(118+114-X)50,解得生长量=16,答案为A。
注:已进水800桶,即原有量为800;所求“每分钟进水多少桶”是使水增多的生长量。
今天的牛顿问题就介绍到这里,希望对备考路上的广大考生有多帮助。