在资料分析的考题中,提到“间隔”首先想到的是间隔增长率,然而间隔基期量、间隔倍数、间隔增长量也是资料分析中常常涉及的与间隔有关系的知识点,接下来我们就来聊一聊资料分析中的“间隔”问题。
什么是“间隔”问题呢?比如现在有三个时期,已知第三期与第二期、第二期与第一期的关系,求第三期与第一期的关系,这样的题目就属于“间隔”问题。接下来我们通过题目来呈现资料分析的“间隔”问题。
一、间隔增长率
题目:2020年某种农作物的产量为700万吨,增长了10%,增速同比提高4个百分点。
问题:2020年某种农作物的产量与2018年相比增速是多少?
分析:此题考查的是2020年比2018年的增长率,中间间隔了2019年,这考察的就是间隔增长率的问题。设2020年比2018年的间隔增长率为R,2020年比2019年的增长率和2019年比2018年的增长率分别为和r1和r2,那么间隔增长率R与r1和r2的关系为: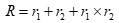 。这就是间隔增长率的公式,是需要我们牢牢记住的。
。这就是间隔增长率的公式,是需要我们牢牢记住的。
解答:题目中2020年比2018年的增长率为间隔增长率R,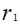 =10%,
=10%,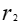 =10%-4%=6%,因此
=10%-4%=6%,因此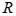 =10%+6%+10%×6%=16.6%,即2020年比2018年的增长率为16.6%。
=10%+6%+10%×6%=16.6%,即2020年比2018年的增长率为16.6%。
二、衍生的“间隔”问题
题目:2020年某种农作物的产量为700万吨,增长了10%,增速同比提高4个百分点。
问题:
①2018年某种农作物的产量是多少万吨?
②2020年某种农作物的产量是2018年多少倍?
③2020年某种农作物的产量比2018年多多少万吨?
分析:
①题:求2018年某种农作物产量的具体数值,题目给的是2020年某种农作物产量,所以此题考查的知识点是间隔基期量。基期量= ,因此间隔基期量=
,因此间隔基期量= 。
。
②题:求2020年某种农作物产量相比于2018年的倍数,所以此题考查的知识点是间隔倍数。倍数=1+增长率,因此间隔倍数=1+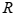 。
。
③题:求2020年某种农作物产量相比于2018年的增长量,所以此题考查的知识点是间隔增长量。增长量=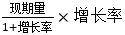 ,当增长率≈
,当增长率≈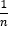 时(特殊分数),增长量=
时(特殊分数),增长量=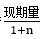 ;因此间隔增长量=
;因此间隔增长量= ,当
,当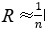 时,间隔增长量=
时,间隔增长量=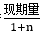 。
。
解答:
①题:2018年某种农作物的产量即间隔基期量=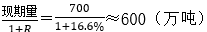 。(备注:在前面已经求过)。
。(备注:在前面已经求过)。
②题:2020年某种农作物的产量相比于2018年的倍数即间隔倍数=1+R=1+16.6%=1.166(倍)。
③题:2020年某种农作物的产量相比于2018年的增长量即间隔增长量= =
=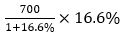 ,此种列式计算量较大,可考虑特殊分数计算增长量。
,此种列式计算量较大,可考虑特殊分数计算增长量。
当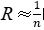 时,间隔增长量=
时,间隔增长量=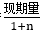 ,因为=16.6%≈
,因为=16.6%≈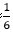 ,所以间隔增长量=
,所以间隔增长量= =100(万吨),此种方法计算量比较简单,推荐利用特殊分数法计算增长量。
=100(万吨),此种方法计算量比较简单,推荐利用特殊分数法计算增长量。
备注:
特殊分数法计算增长量,需要大家熟识常见的特殊分数,如下表:
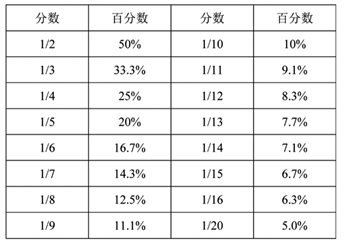

②增长量也可以借助现期量-基期量(前面已经求解出来)≈700-600=100(万吨)。
三、思路总结
关于资料分析的“间隔”问题,大家学会了吗?接下来给大家整理一下思路,见如下思维导图。
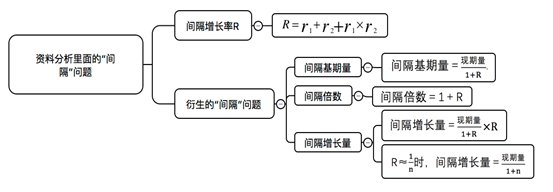
什么是“间隔”问题呢?比如现在有三个时期,已知第三期与第二期、第二期与第一期的关系,求第三期与第一期的关系,这样的题目就属于“间隔”问题。接下来我们通过题目来呈现资料分析的“间隔”问题。
一、间隔增长率
题目:2020年某种农作物的产量为700万吨,增长了10%,增速同比提高4个百分点。
问题:2020年某种农作物的产量与2018年相比增速是多少?

分析:此题考查的是2020年比2018年的增长率,中间间隔了2019年,这考察的就是间隔增长率的问题。设2020年比2018年的间隔增长率为R,2020年比2019年的增长率和2019年比2018年的增长率分别为和r1和r2,那么间隔增长率R与r1和r2的关系为:
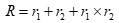 。这就是间隔增长率的公式,是需要我们牢牢记住的。
。这就是间隔增长率的公式,是需要我们牢牢记住的。
解答:题目中2020年比2018年的增长率为间隔增长率R,
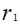 =10%,
=10%,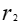 =10%-4%=6%,因此
=10%-4%=6%,因此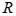 =10%+6%+10%×6%=16.6%,即2020年比2018年的增长率为16.6%。
=10%+6%+10%×6%=16.6%,即2020年比2018年的增长率为16.6%。二、衍生的“间隔”问题
题目:2020年某种农作物的产量为700万吨,增长了10%,增速同比提高4个百分点。
问题:
①2018年某种农作物的产量是多少万吨?
②2020年某种农作物的产量是2018年多少倍?
③2020年某种农作物的产量比2018年多多少万吨?
分析:

①题:求2018年某种农作物产量的具体数值,题目给的是2020年某种农作物产量,所以此题考查的知识点是间隔基期量。基期量=
 ,因此间隔基期量=
,因此间隔基期量= 。
。
②题:求2020年某种农作物产量相比于2018年的倍数,所以此题考查的知识点是间隔倍数。倍数=1+增长率,因此间隔倍数=1+
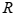 。
。
③题:求2020年某种农作物产量相比于2018年的增长量,所以此题考查的知识点是间隔增长量。增长量=
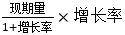 ,当增长率≈
,当增长率≈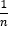 时(特殊分数),增长量=
时(特殊分数),增长量=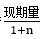 ;因此间隔增长量=
;因此间隔增长量= ,当
,当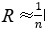 时,间隔增长量=
时,间隔增长量=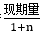 。
。解答:

①题:2018年某种农作物的产量即间隔基期量=
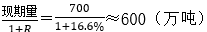 。(备注:在前面已经求过)。
。(备注:在前面已经求过)。
②题:2020年某种农作物的产量相比于2018年的倍数即间隔倍数=1+R=1+16.6%=1.166(倍)。

③题:2020年某种农作物的产量相比于2018年的增长量即间隔增长量=
 =
=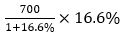 ,此种列式计算量较大,可考虑特殊分数计算增长量。
,此种列式计算量较大,可考虑特殊分数计算增长量。
当
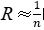 时,间隔增长量=
时,间隔增长量=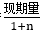 ,因为=16.6%≈
,因为=16.6%≈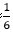 ,所以间隔增长量=
,所以间隔增长量= =100(万吨),此种方法计算量比较简单,推荐利用特殊分数法计算增长量。
=100(万吨),此种方法计算量比较简单,推荐利用特殊分数法计算增长量。备注:
特殊分数法计算增长量,需要大家熟识常见的特殊分数,如下表:


②增长量也可以借助现期量-基期量(前面已经求解出来)≈700-600=100(万吨)。
三、思路总结
关于资料分析的“间隔”问题,大家学会了吗?接下来给大家整理一下思路,见如下思维导图。










