在备战公务员考试的过程中,数量关系往往是对同学们比较困难的版块。工程问题是公务员考试行测数量关系板块中的一类常考题型,基本上属于每年必考的题型。在数量关系版块中,工程问题往往是其中相对较简单的问题,也是同学们相对更容易掌握的题型赋值法,是数学上解决工程问题常用的一类方法相对于数学常用的方程法,因为可以设一个具体的数字,所以在计算上,更加方便,也更加迅速。
那么,如何巧用赋值法解决工程问题,同学们就跟着我一起看一看吧。
在工程问题当中,我们将能用赋值法解决的工程问题分为两类:给定时间型和效率制约型。这两类也是考试中工程问题最常考的类型。
我们先来看看给定时间型的工程问题:
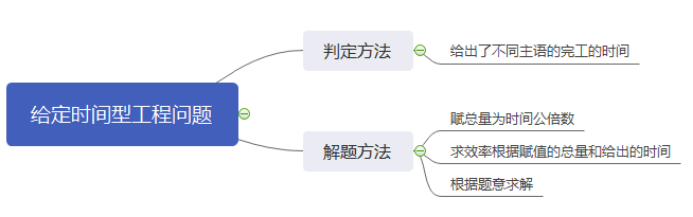
在工程问题中,我们往往将给出了不同主语完工时间的题目称作给定时间型,这类题型我们采用赋值法,通过三步走解决:
第一步:赋总量(为时间的公倍数)
第二步:求效率(根据赋值的总量和给出的时间求出)
第三步:求其他(根据题意求解需求的量)
那么,下面我们通过一道具体的例题运用一下我们的方法。。
【例题】一项工程,已知甲完工时间是4天,乙完工时间是5天,问甲乙合作,多少天可以完成这项工程的90%?
A.1天
B.2天
C.3天
D.4天
【解析】B
第一步,根据甲、乙分别完成这项工程的时间为4天和5天,赋值总量为甲、乙完工时间的公倍数20。
第二步,根据赋值的总量和工作时间,可以得到甲、乙的效率分别为5和4。
第三步,根据题意,甲乙合作效率之和为9,完成这项工程的90%,总量为20,总量的90%即为20×90%=18,得到需要的时间为18÷9=2天。
因此,选择B选项。
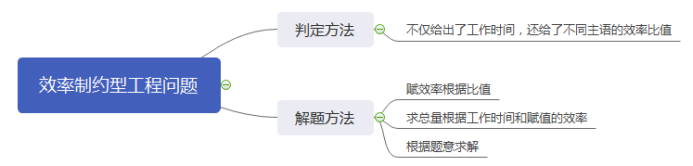
效率制约型的工程问题指的是不仅给出了工作时间,还给出了不同主语效率的比值。效率制约型的工程问题我们同样采用赋值法解题,也有三步走:
第一步:赋效率(根据效率的比值赋值效率)
第二步:求总量(根据赋值的效率和工作时间求出总量)
第三步:求其他(根据题意求解需求的量)
同样,我们根据一道例题来运用一下我们的方法:
【例题】已知甲、乙、丙的效率之比为5:4:3,一项工程由甲先做2天,乙再做4天,最后丙做8天正好完成,问这项工程由甲单独完成需要多少天?
A.10 天
B.12.5天
C.7天
D.16.7天
【解析】A
第一步,根据甲、乙、丙的效率之比为5:4:3,赋值三者的效率分别为5、4、3。
第二步,根据赋值的甲、乙、丙的效率以及这项工程由甲先做2天,乙再做4天,最后丙做8天正好完成,可得工程总量为5×2+4×4+3×8=50。
第三步,根据题意,已求出总量为50,甲的效率为5,可得甲单独完工的时间为10天。
因此,选择A选项。
那么,运用赋值法巧解工程问题,同学们,学会了吗?这类题目大家只要牢记并理解我们三步走的运用,就迎刃而解了。希望同学们都能掌握这类题目,在考场中拿下这关键的1分!
点击预约:【2022国家公务员考试公告职位表提醒】

| 历年国家公务员考试公告 | |||||
| 年份 | 公告发布时间 | 职位表 | 报名时间 | 笔试时间 | 公告详情 |
|---|---|---|---|---|---|
| 2021 | 2020年10月14日 | 2021国家公务员职位表 | 10月15日-24日 | 11月29日 | 查看2021国考公告 |
| 2020 | 2019年10月14日 | 2020国家公务员职位表 | 10月15日-24日 | 11月24日 | 查看2020国考公告 |
| 2019 | 2018年10月21日 | 2019国家公务员职位表 | 10月22日-31日 | 12月2日 | 查看2019国考公告 |
| 2018 | 2017年10月28日 | 2018国家公务员职位表 | 10月30日-11月8日 | 12月10日 | 查看2018国考公告 |










